Time: 4-5 days
- Original request
- Download
- How to Use
- Creek puzzle
- Algorithm - data structure
- Algorithm - satisfying the numbers on line crossing
- Algorithm - callback
- Single area check
Original request
The project was done for functional programming ([SPOP]) course on my university. The task was to write Creek puzzle solver using Haskell. Project is console only.
Download
Dropbox
How to use
- Unpack zip.
- Click on "projekt_SPOP" file in folder.
- After loading the file type "go" in command line.
- Text "Podja nazwe pliku z rozszerzeniem" appears.
- Type in the name of file you want to solve for example "1.txt". It is obligatory to add ".txt" at the end.
- Program displays contents of the file
- Program displays "parsowanie poprawne" if the text file is in a correct format.
- Type "yes" to solve the puzzle
Once solved command line displays solution with 0 marked as empty boxes and 1 marking the filled boxes. Solver is meant for puzzles with small dimensions.
In order for program to use puzzle must be defined in specific format. Folder contains puzzle examples. The format is specified as:
"Creek (height dimension, wide dimension) [(( record, column), number on the line-crossing), ...] "
Program has only minor input data control so it's up to the user to provide proper data. Numbering of records and columns start from 0.
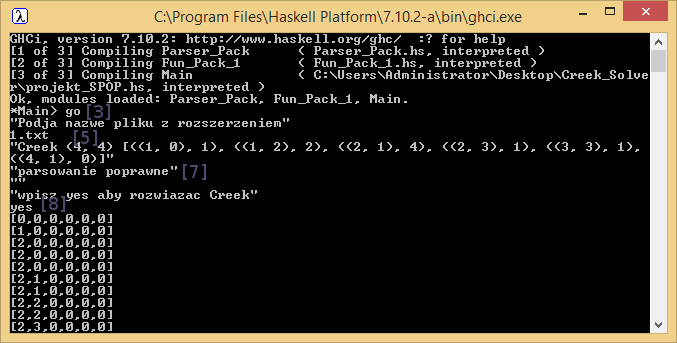
How-to-use as seen in the command line
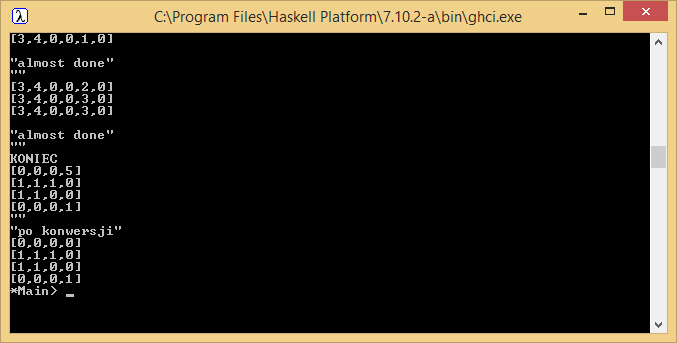
Solution displayed in console
Creek puzzle
The task in a Creek puzzle is to fill boxes. In order for solution to be legal following criteria must be met:
- Number in the crossing determines how many filled boxes must be in the neighbourhood of the number
- Unfilled boxes must create one area
- Filled boxes don't need to be forced to be filled by numbers in the crossing
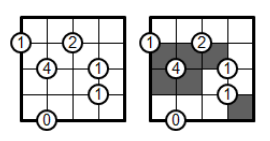
Example of solved creek puzzle
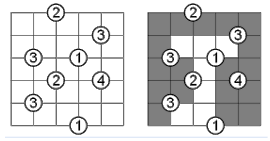
Example of solved creek puzzle with box being filled without being forced by number in the crossing (the upper left corner)
Algorithm - data structure
Warning: while the algorithm itself is easy to understand it's difficult to explain. I hope given examples makes things easier to understand. If you feel any part needs more explaining be sure to ask.
In order to solve Creek puzzle backtracking algorithm was used. It's a little smarter version of brute-force. Firstly program seeks to set filled boxes in such way that numbers in the line crossings are satisfied. Once this is achieved program checks if 0s make one area. If yes then solution has been found otherwise the new field with properly field boxes is being searched.
The field is represented by list of lists. The field contains 3 values:
- 5 - box is neither filled nor empty
- 0 - box is empty as forced by number in the crossing
- 1 - box is filled as forced by number in the crossing
At first field is filled with 5s.
What the program is trying to do is to put the neighbourhood of the number in the crossing (called archetype in the program) into the field when it's legal.
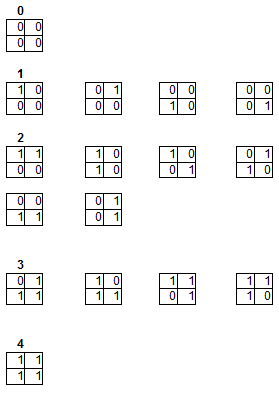
Archetypes for different numbers in the line crossing (bold) - 1s mark filled box, 0 mark empty box
It's ok to insert archetype into the field when numbers in the archetype match numbers on the field or the number on the field is 5 (box can be both empty and filled). If number in the box is 5 after putting archetype on board the value must be changed to the numbers forced by archetype. This is because the number on the crossing forces the boxes in its neighbourhood to be either filled or empty.
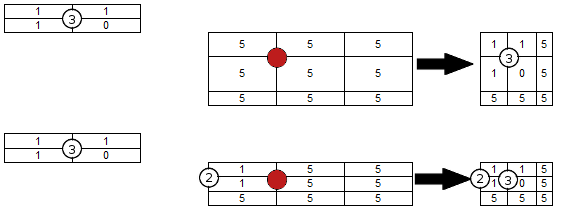 Example of legal putting archetype with 3 in the line crossing in the red spot: Top example shows putting first archetype (since field is filled with 5s only), bottom example shows putting the second archetype. It's ok to put archetype since there is no conflict between 1s already on the field (forced by 2 in the crossing) and 1s and 0s of archetype about to be put. Right side shows field after archetype being applied.
Example of legal putting archetype with 3 in the line crossing in the red spot: Top example shows putting first archetype (since field is filled with 5s only), bottom example shows putting the second archetype. It's ok to put archetype since there is no conflict between 1s already on the field (forced by 2 in the crossing) and 1s and 0s of archetype about to be put. Right side shows field after archetype being applied.It is illegal to put archetype into the field when:
- 1s are outside of the field as you can't fill boxes that don't exist
- 1s and 0s of archetype about to be put don't match with 0s and 1s already on board
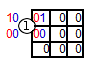
Illegal move (red) - 1s outside of field
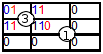
Illegal move (red) - right bottom 0 of archetype doesn't match 1 that is already on board
Algorithm - satisfying the numbers on line crossing
In order to satisfy the numbers in the line crossing program uses special list and a number variable. List stores which archetypes has been put in the field. Number variable keeps index which number in the crossing is being put at the current moment. Information about what is the value of the number in the crossing is kept in another structure along with coordinates (parsed text file data).
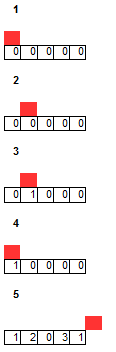
List with number variable (red) at different stages of program
- Start of algorithm - first number on the crossing is being placed with 0th archetype (
- for 0 in the crossing that would be (0,0;0,0)
- for 1 (1,0;0,0)
- for 2 (1,1;0,0)
- for 3 (1,1;1,0)
- for 4 (1,1;1,1)
- for 0 in the crossing that would be (0,0;0,0)
- 0th archetype for first number on the crossing was legal and has been put in. Program moves on to putting the second number on the crossing
- Archetype with index 0 for second number in the crossing was illegal so program tries out archetype with index 1
- Program tried out all archetypes for second number and none of them was legal. Program performs callback - it forces the previous number in the crossing to change it's archetype. If for previous number it was the last available archetype (so there are no more archetypes available) the previous archetype callback forcing the change of archetype on the pre-previous number. This goes until some number have archetypes available.
- Program ends when number variable is pointing at position outside of the list. All numbers in the crossings have been satisfied. On the other hand if it's impossible to find legal archetype for first number in the crossing it means solution doesn't exist.
Algorithm - callback
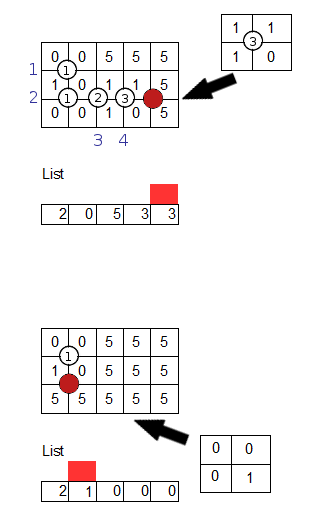
Multi-callbacks example
Program tries to put 5th number on the line crossing with value 3 on the crossing. This is illegal due to upper-left corner (0 in the field and 1 in the archetype). It's the last archetype available for number 3 so callback is performed. Blue numbers show the order at which numbers were placed. 4th number can't change archetype because it is out of archetypes so it calls callback. 3rd is out as well so it callbacks. 2nd number has some archetypes available so callback stops there.
Callback forces to change field so that only numbers on the left from the red square are applied. This is done by generating new field with 5s only and applying the archetypes of number in the crossings only to the left of the red square. In this example. Only archetype with index 2 for number 1 on crossing is applied to the field.
The bottom picture shows which archetype will be tested in the next iteration (after callbacks) and for which number.
Single area check
After program satisfies numbers in the cross lines constrain it needs to check if 0s make single area. It is done using grow region algorithm. If you need further reading on grow region algorithm you can go to wikipedia or 4th part of my Zerg infection guide (as it works similar).
The idea for checking if 0s make up a single region is to change 0s into 1s starting from single 0 and at the end checking if there are any 0s left. At first a 0 is picked from the field - any 0 will do. That box is added to the list and its value is changed to 1. List contains 1s that will check neighbourhood for 0s and 5s to change into 1. We consider 5s because they can be both 0s and 1s - they can serve as a bridge between 0s. We need to make a copy of the field as original will be needed later.
In each iteration head of the list is picked. For the box from the head neighbourhood of the box is checked in search of 0s and 5s. If there are any they are changed into 1s and added to the list. Head of the list is then removed. Algorithm does it until there is something in the list.

Single area check algorithm in a pictures
Once algorithm is done program counts number of 0s in the field. If count is equal to zero that means 0s make a single area, with possible 5s serving as bridges. Program again does the region grow this time changing 0s into 7s. This shows which 5s are supposed to be turned into 0s. After it is done 7s are turned into 0s and 5s(not serving as bridges) into 1s. Print the solution and be happy.
If count of 0s is bigger than 0 this means that potential solution doesn't meet single area criteria. In this case solution is ignored. Red square is moved to the last position in the list. New field is created and then all archetypes of numbers in the crossing lines are applied except the last one. Index for last number is increased by one or callback is called if required. All these actions can be summarized as a callback called from the extra number if list had one more number.
Thank you for reading. If you have any questions be sure to ask on Newgrounds, Twitter or in the comments below.
Tags: Creed, puzzle, sudoku, solver, Haskell, functional programming, logical